Formal methods in control design for nonlinear systems are often focused on the stabilization of an equilibrium. Modern robotics applications, however, require notions of stability to be defined when tracking reference trajectories. The idea behind an incremental region of attraction is that as long as an attractive region can be defined around any trajectory within some operating regime then all initial conditions of the system that start within the region converge to the trajectory asymptotically or exponentially. The synthesis of the region involves the verification of an incremental Lyapunov function using a branch-and-cut approach as shown below. Once a suitable incremental region of attraction is found, the attractive region around any trajectory can be efficiently computed. For example, the figure below shows the attractive region around a swing-up trajectory of a torque-limited inverted pendulum. The blue lines indicate simulations started randomly within the attractive region. 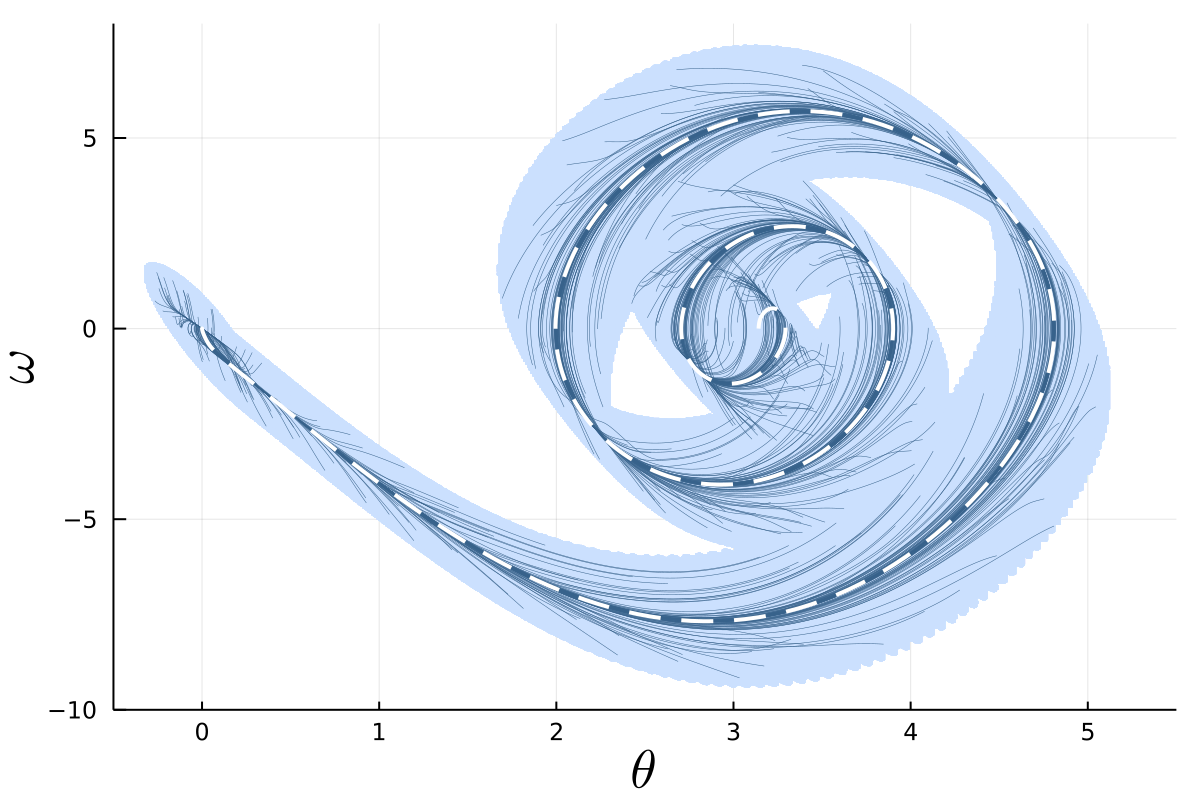 Some of the randomized simulations plotted above are animated in the following GIF.
Some of the randomized simulations plotted above are animated in the following GIF.  This is currently unpublished work, please watch this space for more information.
This is currently unpublished work, please watch this space for more information.
Contraction theory is a tool to analyze incremental stability properties for nonlinear systems and constructively design tracking controllers that stabilize the system around any trajectory. In (Zhao et al. (2021)), we provide synthesis procedures to compute robust control contraction metrics that minimize the -gain from the disturbances to the tracking error. Even better performance can be acheived by augmenting the contraction theory-based setup with the -adaptive control architeture to compensate for the disturbances within the control channel (Lakshmanan et al. (2020)). We provide certificates in the form of tubes whose width is adjustable based on the adaptive controller parameters. Furthermore, they can be incorporated into motion planners to provide paths that are safe with respect to the disturbances, as shown below. The figure illustrates the path of 10 unicycle systems with randomized initializations that remain within the tube and avoid collisions with the gray obstacles. 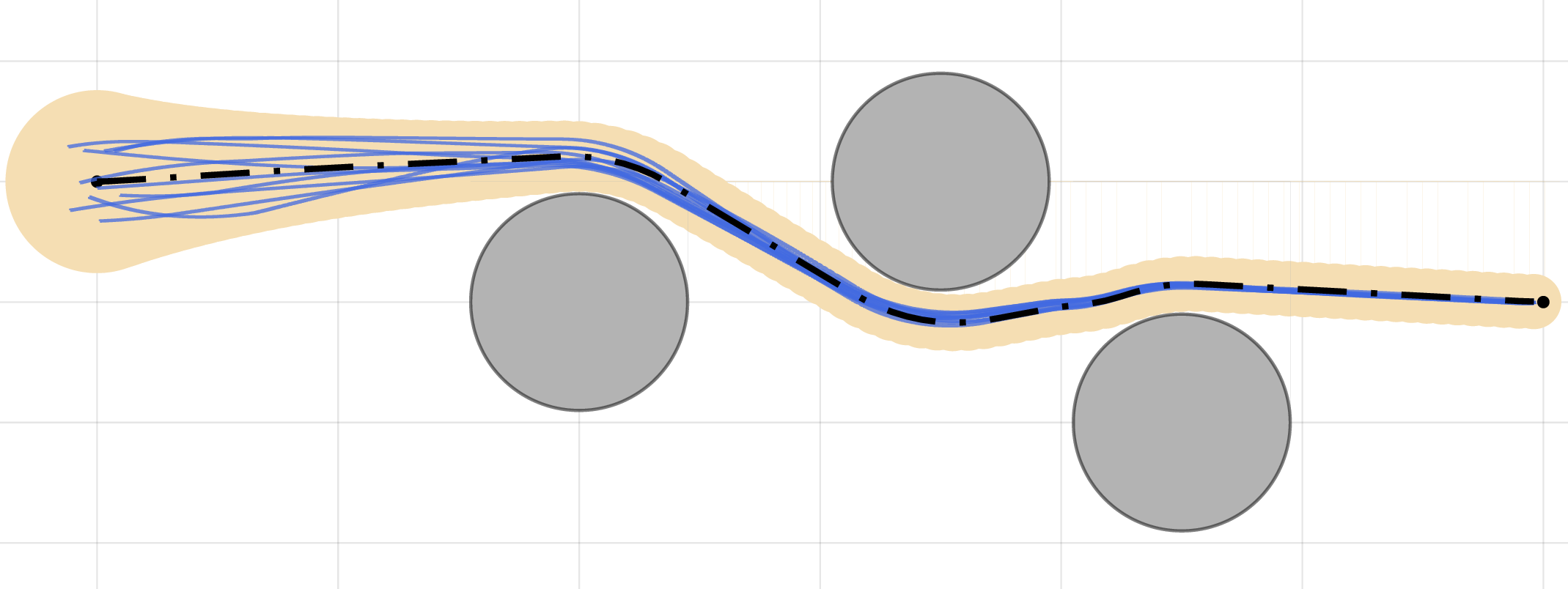 While the tubes are tunable based on tracking requirements, their adjustment relies on a trade-off with the inherent robustness of the system to model inaccuracies. In (Lakshmanan et al. (2021)), we show that the performance of the contraction theory-based -adaptive control architecture can be improved by learning any unmodeled dynamics in the system without sacrificing robustness. The GIF below illustrates the improvement in the peformance a vehicle traversing a race track in the form of tighter tubes.
While the tubes are tunable based on tracking requirements, their adjustment relies on a trade-off with the inherent robustness of the system to model inaccuracies. In (Lakshmanan et al. (2021)), we show that the performance of the contraction theory-based -adaptive control architecture can be improved by learning any unmodeled dynamics in the system without sacrificing robustness. The GIF below illustrates the improvement in the peformance a vehicle traversing a race track in the form of tighter tubes. 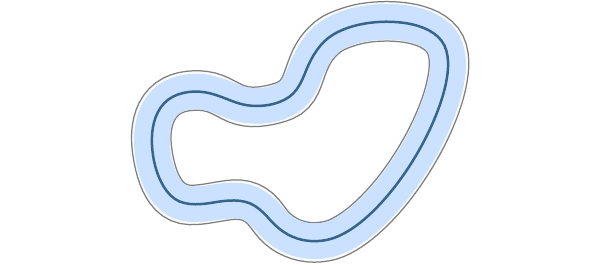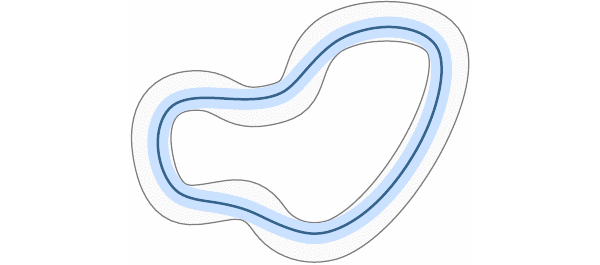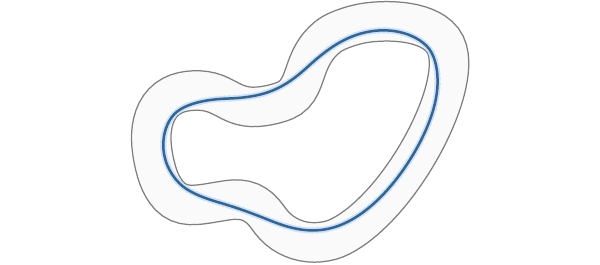 In the video below, we show the performance of an -adaptive control augmentation to the tracking control of a quadrotor by injecting disturbances in several scenarios (Wu et al. (2021)).
In the video below, we show the performance of an -adaptive control augmentation to the tracking control of a quadrotor by injecting disturbances in several scenarios (Wu et al. (2021)).
A. Lakshmanan[1], A. Gahlawat[1], N. Hovakimyan. "Safe Feedback Motion Planning: A Contraction Theory and -Adaptive Control Based Approach." Proceedings of the 59th IEEE Conference on Decision and Control (CDC), pp. 1578-1583, 2020.
A. Lakshmanan[1], A. Gahlawat[1], L. Song, A. Patterson, Z. Wu, N. Hovakimyan, E. Theodorou. "Contraction -Adaptive Control using Gaussian Processes." Proceedings of the 3rd Conference on Learning for Dynamics and Control, pp. 1027-1040, 2021.
P. Zhao, A. Lakshmanan, K. Ackerman, A. Gahlawat, M. Pavone, & N. Hovakimyan. "Tube-certified trajectory tracking for nonlinear systems with robust control contraction metrics." Under review at ICRA 2022.
Z. Wu, S. Cheng, K. Ackerman, A. Gahlawat, A. Lakshmanan, P. Zhao, & N. Hovakimyan." Adaptive Augmentation for Geometric Tracking Control of Quadrotors." Under review at ICRA 2022.
| [1] | Equal contribution |
Collision checking is a computational bottleneck in motion planning problems. While there exist several fast methods for exact collision checking between convex objects, collision checking for trajectories are generally more ad-hoc — they are typically checked pointwise up to some resolution. In (Lakshmanan et al. (2019)), we provide fast methods to check for collisions for absolutely continuous curves. In the video below, we describe the prodcedure at a high-level, and show an example of how such methods may be employed in sampling-based planning. The collision detection is extensible to situations when only a probabilistic model of the motion of an obstacle is available as a high-probability result (Patterson et al. (2020)). The following figure shows two paths (green and blue), one of which has a higher probability collision than another with an obstacle. The motion of the obstacle is predicted using a gaussian process model based on past data and probabilistic intention. 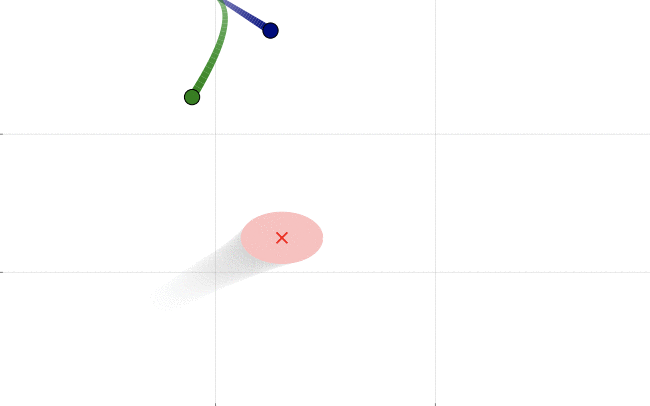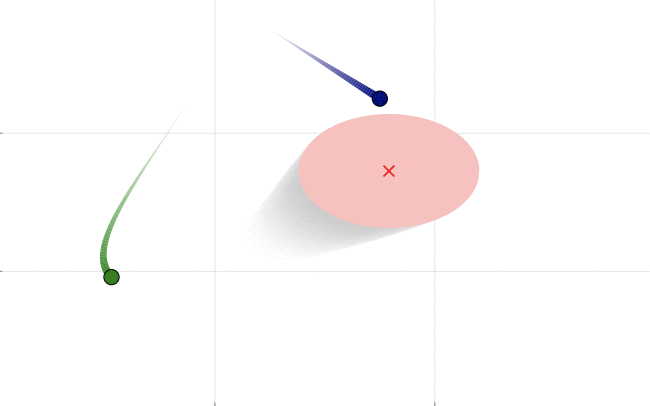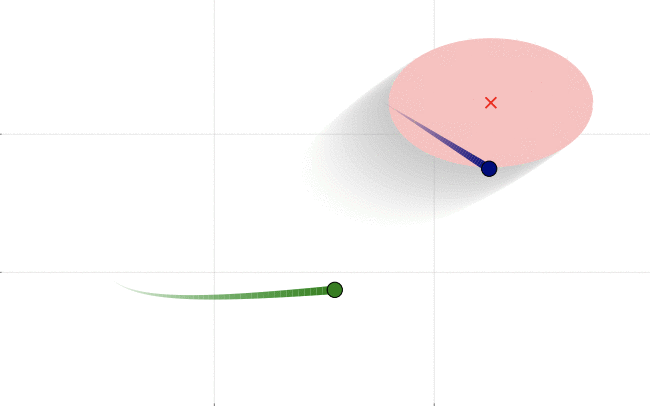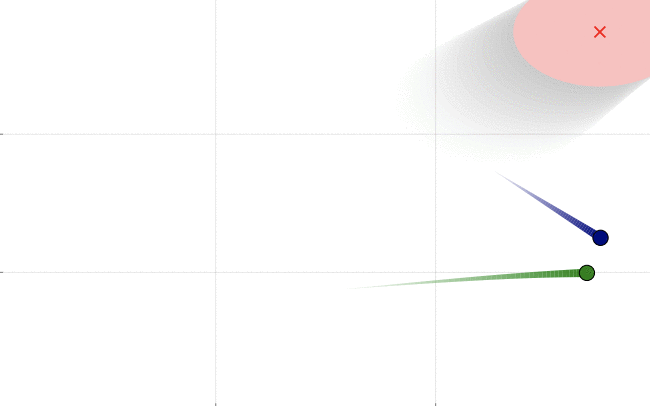
A. Lakshmanan, A. Patterson, V. Cichella, N. Hovakimyan. "Proximity Queries for Absolutely Continuous Parametric Curves." Proceedings of Robotics: Science and Systems XV, 2019.
A. Patterson, A. Lakshmanan, N. Hovakimyan. "Intent-Aware Probabilistic Trajectory Estimation for Collision Prediction with Uncertainty Quantification." Proceedings of the 58th IEEE Conference on Decision and Control (CDC), pp. 3827-3832, 2019.